كان للعلماء العرب الفضل في وضع البذور الأولى لمعظم العلوم التي برع فيها الغرب الآن، فهم من زرعوا ونحن من نحصد ونستفيد من علمهم وبحوثهم وما توصلوا إليه من استكشافات وعلوم، على الرُّغم من انعدام الإمكانات والتكنولوجيا التي يعتمد عليها العلماء في يومنا.
منهم
"أبو عبد الله محمد بن موسى الخوارزمي" الذي يعد من أشهر علماء العرب وأبرزهم في الفلك، ومن أوائل علماء الرياضيات، كما برع في علم الجغرافيا.
أهم إنجازاته
[list=rtl][*]أنشأ الخوارزمي علم الجبر، وقدم الكثير من النظريات الهامة في علم الرياضيات.
[*]ساهم الخوارزمي في تَرْجَمَة الأرقام العربية والترقيم الهندي ونقله إلى أوروبا.
[*]طور في خطوات الكثير من المسائل والمعادلات في الجبر.
[*]أضاف الخوارزمي مفهوم الصفر في الرياضيات، كما وضع المواقع العشرية في الأعداد.
[*]كان الخوارزمي ضمن مجموعة العلماء الذين قاموا برسم خريطة للعالم لأول مرة في عهد المأمون.
[*]كما يرجع له الفضل في مساعدة العلماء في حل المعادلات التربيعية والخطية الخاصة بالهندسة البديهية بواسطة علم الجبر.
[*]كما تمكن الخوارزمي من حساب العديد من الأحجام الهندسية.
[/list]
محمد بن موسى الخوارزمي
كان حدث تأليف كتاب الجبر والمقابلة بالغ الأهمية واعترف به المؤرخون القدامى المحدثون على السواء كما لم تخف أهمية هذا الكتاب على علماء ورياضيي تلك الحقبة إذ لم يتأخر الرياضيون حتى أثناء حياة الخوارزمي
هو عبد الله بن محمد بن موسى الخوارزمي، أصله من خوارزم بأوزبكستان، لا يعرف الكثير عن حياته سوى أنه كان يعيش في بغداد في عهد الخليفة المأمون حوالي 813 إلى 833م وكان مشرفا على مكتبة المأمون وقد خلف العديد من الكتب منها: كتابا الزيج الأول والثاني، كتاب الرخامة، كتاب عمل الإسطرلاب، كتاب الجمع والتفريق، كتاب الجبر والمقابلة. أما أشهر كتبه وأهمها فهو كتاب: الجبر والمقابلة وقد كان الخوارزمي مهتما بعلم الفلك أيضا وشغل عضوية في اللجنة التي كلفت بقياس درجة من درجات محيط الأرض غير أن الخوارزمي حاز على شهرته الأساسية في مجال الرياضيات وفي الجبر بصفة خاصة.
وقد انتهت المعادلة عند الخوارزمي إلى ست مسائل؛ لأن المعادلة بين عدد وجذر ومال مفردة أو مركبة تجيء ستة:1-أموال تعدل جذورًا
2- أموال تعدل عددًا
3- جذور تعدل عددًا
4- أموال وجذور تعدل عددًا
5- جذور وعدد تعدل أموالاً
6- أموال وعدد تعدل جذورًا
ومن كتبه وابحاثه
كتاب المختصر في حساب الجبر والمقابلة
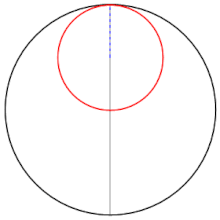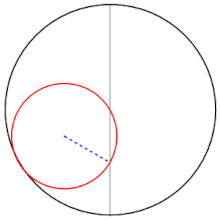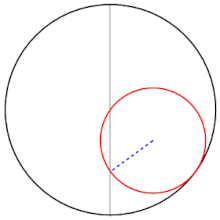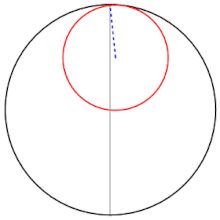
صفحات من القرن الرابع عشر تُظهر حلولاً هندسية لمعادلتين تربيعيتين
الكتاب يحتوي على كل ما هو مفيد في حساب ما يحتاجه الناس في مسائل الميراث، ومشاكل التقسيم، والتقاضي، والتجارة، وبشكل عام لجميع العلاقات المتبادلة أو أيضًا في مسح الأراضي وحفر القنوات والحسابات الهندسية وأشياء أخرى متنوعة حيث ينقسم الكتاب إلى ثلاثة أجزاء:
- منهج ومعالجة معادلات الدرجة الأولى والثانية وهو الجزء الرئيسي من الكتاب.
- منهج لحساب المساحات والأحجام لبعض الأشكال الهندسية.
- حل مسائل الميراث والوصايا والتكمّلة والرق في الإسلام
وفي هذه الأطروحة، دراسة منهجية لمجموعة من المعادلات، وتغطي هذه الدراسة الحلول الكاملة لمعادلة رياضية، وتختلف طريقة وصف المعادلات في الكتاب عن الطريقة الحديثة للرياضيات حيث يتم عرضها بالمقادير الجبرية وهي المقادير أو الأعداد التي يحتاج إليها في حساب الجبر والمقابلة وهي ثلاثة على نحو التالي:
- مال: كل ما اجتمع من الشيء المضروب في نفسه ويرمز له x 2
.
- شيء أو جذر: وهو العدد المجهول والذي يرمز له في الرياضيات الحديثة x
.
- عدد مفرد: كل ملفوظ من العدد بلا نسبة إلى جذور ولا أموال ويعرف بالحد الخالي من x .
وللتوضيح يمكن ضرب المثال التالي كما هو معرف في بالشكل الحديث:
a x 2 + b x + c = 0
وأغلب ما ورد في كتب هي مسائل معادلاتها من الدرجة الأولى أو الثانية والتي صيغتها العامة بحسب المصطلح الرياضيات الحديثة حيث أنّ ( a
، b
، c
) أعداد معلومة وهي:
a
وهو عدد الأموال وهو معامل x 2
. b
وهو عدد الأشياء أو الجذور التي يحتاج إلى استخراجها ونرمز له بـ x
c
وهو العدد المفرد والذي ندعوه بالثوابت وهو الحد الخالي من x
.
ويمكن شرح ما سبق بالإشارة إلى أبيات الشعر لابن الياسمين في الأرجوزة الياسمينية:
عَلى ثَلاثَةٍ يدورُ الجَبرُالمالُ والأعدادُ ثُمَّ الجذرُفالمالُ كلُّ عَدَدٍ مُربَّعِوَجَذرُهُ واحِدُ تِلكَ الأضلُعِوالعَدَدُ المُطلَقُ مَا لَم يُنسبلِلمالِ أَو للجَذرِ فافهَم تُصِبوالشَّيءُ والجَذرُ بمَعنَى واحِدٍكَالقُولِ في لَفظِ أبٍ وَوالِدِومما يلاحظ بأنّ جميع المعادلات والعمليات الحسابية المذكورة في الكتاب يتم وصفها عن طريق صياغة الجمل باستخدام المقادير الجبرية وأيضاً في ذلك الوقت لم يكن معروفاً عند علماء الرياضيات الأعداد السالبة مما أدى به إلى التمييز بين ستة حالات التي تكون فيها الأعداد a
، و b
و c
كلها موجبة:
- الأموال التي تعدل الجذور: ( a x 2 = b x
)
- الأموال التي تعدل العدد: ( a x 2 = c
)
- الجذور التي تعدل عدداً: ( b x = c
)
- الأموال والجذور التي تعدل العدد: ( a x 2 + b x = c
)
- الأموال والعدد التي تعدل الجذور: ( a x 2 + c = b x
)
- الجذور والعدد التي تعدل الأموال: ( b x + c = a x 2
)
أي معادلة من الدرجة الأولى أو الثانية يمكن تحويلها إلى إحدى الحالات الست المذكورة أعلاه بمعاملات موجبة. لهذا، استخدم الخوارزمي التقنيتين التي أعطت اسمها للكتاب: «الجبر» و«المقابلة»، الجبر والمقابلة هما جانبان مما يصطلح اليوم بـ«التحويل».
الجبر
الجبر بمعنى «إصلاح الكُسر»
، حيث تم نقل الكلمة إلى اللاتينية، وأصبحت
algebra. الجبر هو تبسيط المعادلة من خلال إزالة الطرح وهذا بإضافة حدود في طرفيها. أي بالمصطلح الحديث الحصول على معادلة بمعاملات موجبة.
مثال :x2 = 40
x − 4
x2 تحول بالجبر إلى x
2 + 4x
2 = 40x
، ثم إلى 5x
2 = 40x
. في الواقع، سمى الخوارزمي الحدود المطروحة (مثل
2 × 4 في المثال السابق): «ناقص». الكلمة المستخدمة هي نفسها للدلالة على أطرافه لمبتوري الأطراف. وبالتالي الجبر هو استعادة ما هو مفقود في المعادلة.
المقابلة
إزالة الطرح بالجبر ليس كافيا للحصول على إحدى الحالات الست.
مثال :x2 + 5 = 40
x + 4
x2 يحتوي على مربعات في كلا الطرفين، ولكن كل طرف هو مجموع
المقابلة تتمثل في طرح كمية من نفس النوع (الدرهم، جذر أو مربع) بحيث لا يبقى منه في الجانبين من المعادلة في نفس الوقت.
مثال :في المعادلة التالية:
x2 + 5 = 40
x + 4
x2 ، نطرح
x2 للحصول على 5 = 40
x + 3
x2.
العضو الأكثر نشاطاً هذا اليوم 
.gif "Tomato")
السمعه♛»
موضوع: فعاليه عظماء العلماء العرب 
.gif "bnfsj")
